A Deadhead Plot
Here’s an interesting plot:
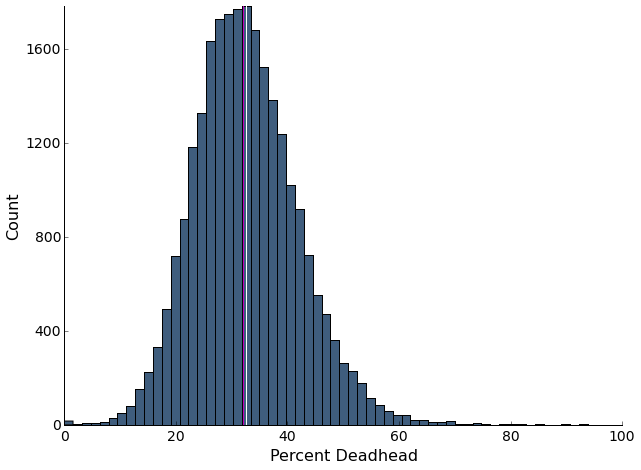
In traditional fixed route transit planning, deadheading usually refers to portions of the route that are not in service: say, going from base to the first stop. However, since paratransit exists in a slightly different paridigm where routes are flexible and the pickup and dropoff locations of riders are known, deadheading refers to any portion of the route without a rider. Given that any increase in time that buses have to be out increases system costs, and deadheading itself doesn’t actively service anyone, deadheading is a necesary evil that needs to be minimized.
Since our data has a row for each action (pickup, dropoff, getting gas, going to base etc.), ETA, and the number of passengers on the bus at the time of the action, I was able to sum the time that each deadheading row took and divide that by the total time for each run. This plot shows the number of buses that don’t have passengers for a certain percentage of their route in our cleaned 4 month dataset. It also demonstrates that this data is relatively normal around a mean/median of around 32%, with a number above 50%.
In theory, this plot would suggest the existance of a certain type of ugly ride: rides that require that the bus deadhead out far from other riders to service someone. However, we haven’t quite figured out a way to relate the costs of deadheading with specific riders in our ugly ride analysis. To demonstrate the problem, imagine there was a ride in Fall City that carried one rider for a single mile. However, to service this ride, the bus had to travel 10 miles from the bulk of the riders that are being picked up and dropped off, and then back after servicing the ride. In this case, it’s fairly clear that all the deadheading time should be associated with the single ride.
However, consider another case in which there was another rider another three miles further out after the last rider. In this case, the portioning out is more complicated. Add in a second dimension, and we haven’t been able to figure out a non arbitrary way of portioning this deadheading cost.